​三角形的面积公式是什么,三角形的面积计算公式是什么?

三角形的面积公式是什么,三角形的面积计算公式是什么?

本文目录

1.三角形的面积计算公式是什么? 2.三角形面积计算公式是什么? 3.正三角形面积的计算公式怎么推理 4.三角形的面积公式是什么

三角形的面积计算公式是什么?

三角形的面积计算公式：

1、已知三角形底a，高h，则S＝ah/2。

2、已知三角形三边a、b、c，则s=1/4*√[2（a^2b^2+ a）（p – b）（p – c）] （海伦公式）（p=（a+b+c）/2）。

3、已知三角形两边a、b，这两边夹角C，则S＝absinC/2，即两夹边之积乘夹角的正弦值。

4、设三角形三边分别为a、b、c，内切圆半径为r，则三角形面积=（a+b+c）r/2。

5、设三角形三边分别为a、b、c，外接圆半径为R，则三角形面积=abc/4R。

三角形简介：

三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用。

常见的三角形按边分有普通三角形（三条边都不相等），等腰三角（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

三角形面积计算公式是什么?

三角形的面积公式：

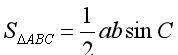
正弦定理三角形面积公式：S=1/2absinc，已知三角形两边a，b，这两边夹角为C，三角形面积公式即两夹边之积乘夹角的正弦值再除以2。

正弦定理指出了任意三角形中三条边与对应角的正弦值之间的一个关系式，由正弦函数在区间上的单调性可知，正弦定理非常好地描述了任意三角形中边与角的一种数量关系。

三角形角的性质：

1、在平面上三角形的内角和等于180°（内角和定理）。

2、在平面上三角形的外角和等于360° (外角和定理)。

3、在平面上三角形的外角等于与其不相邻的两个内角之和。

4、一个三角形的三个内角中最少有两个锐角。

正三角形面积的计算公式怎么推理

正三角形面积公式为：

S=(√3)a²/4，（S是三角形的面积，a是三角形的边长）

1、三角形面积公式为：S=(1/2)ah （S是三角形的面积，a是三角形的一条边，h是这条边上的高）

2、正三角形，三条边相等，三条边上的高也对应相等，边长为a，高为h，则h=(√3)a/2所以可推导出正三角形的面积S=(1/2)ah=(√3)a²/4

等边三角形（又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。等边三角形是特殊的等腰三角形，所以等边三角形拥有等腰三角形的一切性质。

扩展资料

性质

（1）等边三角形是锐角三角形，等边三角形的内角都相等，且均为60°。

（2）等边三角形每条边上的中线、高线和角平分线互相重合。（三线合一）

（3）等边三角形是轴对称图形，它有三条对称轴，对称轴是每条边上的中线、高线 或角的平分线所在的直线。

（4）等边三角形重心、内心、外心、垂心重合于一点，称为等边三角形的中心。（四心合一）

三角形的面积公式是什么

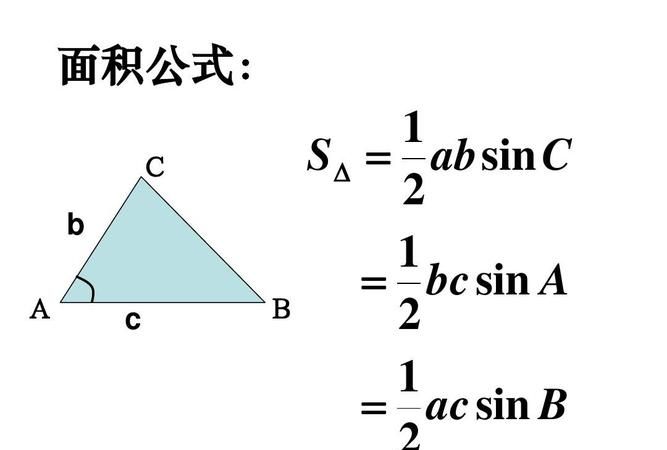
三角形的面积公式：S=1/2ab*sinC

(其中，a、b为三角形两边，C为边c所对角)

因为该公式涉及到建立在直角三角形基础上的正弦值，而“正弦”摆脱圆的控制而在直角三角形中讨论。

已知三角形两边为a，b，且两边夹角为C，则三角形面积为两边之积乘以夹角的正弦值，即S=(absinC)/2。

设三角形三边分别为a，b，c，内切圆半径为r，则三角形面积S=(a+b+c)r/2。

扩展资料

三角形的稳定性使其不像四边形那样易于变形，有着稳定、坚固、耐压的特点。三角形的结构在工程上有着广泛的应用。许多建筑都是三角形的结构，如：埃菲尔铁塔，埃及金字塔等等。

其他的三角形面积公式如因坐标系和行列式概念出现在17世纪，而完善更是18世纪以后的事情，因此，这个公式至少是出现在18世纪的。

以上就是关于三角形的面积公式是什么,三角形的面积计算公式是什么?的全部内容，以及三角形的面积公式是什么的相关内容,希望能够帮到您。